Example 1 Finding The Orthogonal Projection Of A Vector Onto A Plane

By edogawajpn On Sep 28, 2024 Last updated

Example 1 Finding The Orthogonal Projection Of A Vector Onto A Plane To say that xw is the closest vector to x on w means that the difference x − xw is orthogonal to the vectors in w: figure 6.3.1. in other words, if xw ⊥ = x − xw, then we have x = xw xw ⊥, where xw is in w and xw ⊥ is in w ⊥. the first order of business is to prove that the closest vector always exists. I am trying to find the orthogonal projection of a vector $\vec u= (1, 1,2)$ onto a plane which has three points $\vec a=(1,0,0)$, $\vec b=(1,1,1)$, and $\vec c=(0,0,1)$. i started by projecting $\vec u$ onto $\vec a$ and projecting the same vector onto $\vec c$ and finally adding both projections ,but i am not getting what i am expecting. can.

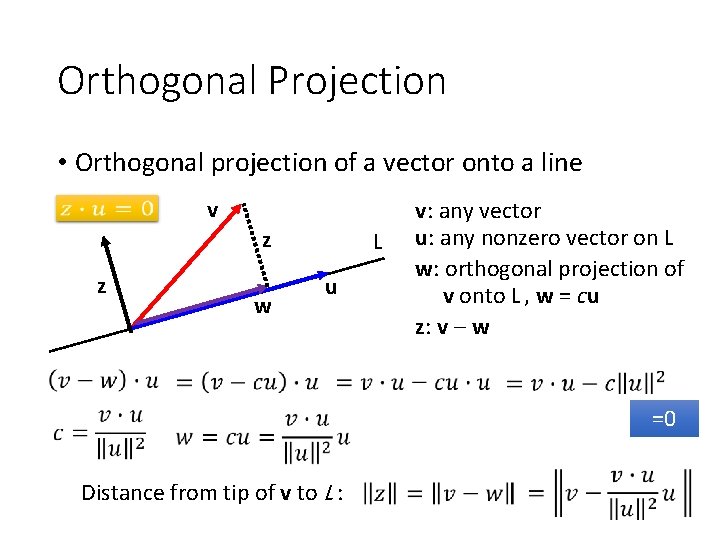
Orthogonal Projection Of A Vector Onto A Plane Youtube Definition. a matrix p is an orthogonal projector (or orthogonal projection matrix) if p 2 = p and p t = p. theorem. let p be the orthogonal projection onto u. then i − p is the orthogonal projection matrix onto u ⊥. example. find the orthogonal projection matrix p which projects onto the subspace spanned by the vectors. Example(projection onto a line in r 3 ) when a is a matrix with more than one column, computing the orthogonal projection of x onto w = col (a) means solving the matrix equation a t ac = a t x. in other words, we can compute the closest vector by solving a system of linear equations. The vector ax is always in the column space of a, and b is unlikely to be in the column space. so, we project b onto a vector p in the column space of a and solve axˆ = p. projection in higher dimensions in r3, how do we project a vector b onto the closest point p in a plane? if a and a2 form a basis for the plane, then that plane is the. Remember that the projection formula given in proposition 6.3.15 applies only when the basis w1, w2, …, wn of w is orthogonal. if we have an orthonormal basis u1, u2, …, un for w, the projection formula simplifies to. ˆb = (b ⋅ u1) u1 (b ⋅ u2) u2 … (b ⋅ un) un. if we then form the matrix.

Find An Orthogonal Projection Of A Vector Onto A Plane Given An The vector ax is always in the column space of a, and b is unlikely to be in the column space. so, we project b onto a vector p in the column space of a and solve axˆ = p. projection in higher dimensions in r3, how do we project a vector b onto the closest point p in a plane? if a and a2 form a basis for the plane, then that plane is the. Remember that the projection formula given in proposition 6.3.15 applies only when the basis w1, w2, …, wn of w is orthogonal. if we have an orthonormal basis u1, u2, …, un for w, the projection formula simplifies to. ˆb = (b ⋅ u1) u1 (b ⋅ u2) u2 … (b ⋅ un) un. if we then form the matrix. Definition 4.11.1: span of a set of vectors and subspace. the collection of all linear combinations of a set of vectors {→u1, ⋯, →uk} in rn is known as the span of these vectors and is written as span{→u1, ⋯, →uk}. we call a collection of the form span{→u1, ⋯, →uk} a subspace of rn. consider the following example. The formula for the orthogonal projection let v be a subspace of rn. to nd the matrix of the orthogonal projection onto v, the way we rst discussed, takes three steps: (1) find a basis ~v 1, ~v 2, , ~v m for v. (2) turn the basis ~v i into an orthonormal basis ~u i, using the gram schmidt algorithm. (3) your answer is p = p ~u i~ut i. note.

Orthogonal Vector Hungyi Lee Orthogonal Set A Set Definition 4.11.1: span of a set of vectors and subspace. the collection of all linear combinations of a set of vectors {→u1, ⋯, →uk} in rn is known as the span of these vectors and is written as span{→u1, ⋯, →uk}. we call a collection of the form span{→u1, ⋯, →uk} a subspace of rn. consider the following example. The formula for the orthogonal projection let v be a subspace of rn. to nd the matrix of the orthogonal projection onto v, the way we rst discussed, takes three steps: (1) find a basis ~v 1, ~v 2, , ~v m for v. (2) turn the basis ~v i into an orthonormal basis ~u i, using the gram schmidt algorithm. (3) your answer is p = p ~u i~ut i. note.

Enter a world where style is an expression of individuality. From fashion trends to style tips, we're here to ignite your imagination, empower your self-expression, and guide you on a sartorial journey that exudes confidence and authenticity in our Example 1 Finding The Orthogonal Projection Of A Vector Onto A Plane section.

Example 1: Finding the orthogonal projection of a vector onto a plane

Example 1: Finding the orthogonal projection of a vector onto a plane Projection of a vector onto a plane Calculus 3 - Vector Projections & Orthogonal Components Example 1: Finding the orthogonal projection of a vector onto another vector Orthogonal projection of a vector onto a plane. Find an Orthogonal Projection of a Vector Onto a Plane Given an Orthogonal Basis (R3) 13.7. Projections. Example of projection on a plane in R3 Projection into Subspaces Projection onto plane Finding standard matrix of orthogonal projection onto a plane Linear Algebra 6.2.2 Orthogonal Projections 4.2 Projection onto a Plane Example Projection of a vector onto a vector Visualizing a projection onto a plane | Linear Algebra | Khan Academy Vector Projections Vector Projections | Vector Calculus #17 Linear Algebra - Examples of Orthogonal Projections Orthogonal projection of a vector onto a line. Orthogonal Projections (Example) Projection of a vector onto a subspace

Conclusion

Having examined the subject matter thoroughly, one can conclude that write-up offers beneficial knowledge on Example 1 Finding The Orthogonal Projection Of A Vector Onto A Plane. In the entirety of the article, the commentator displays considerable expertise on the subject. In particular, the discussion of this feature stands out as a crucial point. To add to that, the essay does a great job in explaining complex concepts in an easy-to-understand manner. Besides, the scribe features applicable examples that amplify the engagement. An extra component that makes this publication unique is the elaborate review of numerous aspects related to Example 1 Finding The Orthogonal Projection Of A Vector Onto A Plane. The content creators exacting approach makes certain that observers acquire a full grasp of the subject matter. Thank you for perusing this post. Should you require additional details, feel encouraged to reach out to me via the provided contact form. I look forward to your feedback. In summing up, if you want to explore further, listed below are multiple linked articles that you will find enlightening:Wishing you enjoyable reading!